After trying & failing to reproduce the results in the paper “New Insights on the Physical Nature of the Atmospheric Greenhouse Effect Deduced from an Empirical Planetary Temperature Model” by Ned Nikolov & Karl Zeller in which they argue that global temperature is purely a function of solar intensity and atmospheric pressure, I worked out some simplifications that would allow me to apply the standard greenhouse effect.
The key was the paper by Robinson & Catling: “Common 0.1 bar tropopause in thick atmospheres set by pressure-dependent infrared transparency” in which they point out that most planets seem to have their tropopause at a pressure of 0.1bar.
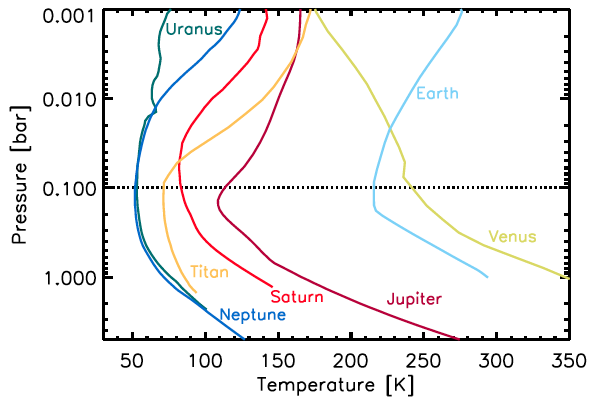 This allowed me to make a rash simplification: that the “top of the atmosphere” was at 0.1bar and/or the tropopause (if temperature profile not specified) on all planets. Next I just need to know the lapse rate which can be readily calculated as g/(specific heat capacity Kj per kg). The specific heat capacity of many gases is about 1, meaning the global temperature is:
This allowed me to make a rash simplification: that the “top of the atmosphere” was at 0.1bar and/or the tropopause (if temperature profile not specified) on all planets. Next I just need to know the lapse rate which can be readily calculated as g/(specific heat capacity Kj per kg). The specific heat capacity of many gases is about 1, meaning the global temperature is:
Planet Temperature = blackbody temp. + 0.1bar height x lapse – Z Log2 (%GHG)
where temp in K, height in km, lapse in C/km & Z is a constant.
Note, on planets where atmospheric pressure was below 0.1bar, the effective tropopause was set to ground level and greenhouse gas concentration ignored.
I started with the short list of bodies from Nikolov & Zeller and included any others where I found information easily available. I had to omit the moon because (unlike Nikolov & Zeller) I was unable to find an agreed figure for average temperature. I also had to omit Saturn for lack of data on its atmosphere profile (I don’t think we know where the bottom is!).
I considered removing Enceladus (a moon of Saturn) as there is evidence it is geologically active or heated by tides – but as this is a potential cause of error of all bodies and the main evidence seems to be the temperature discrepancy itself, I left it in.
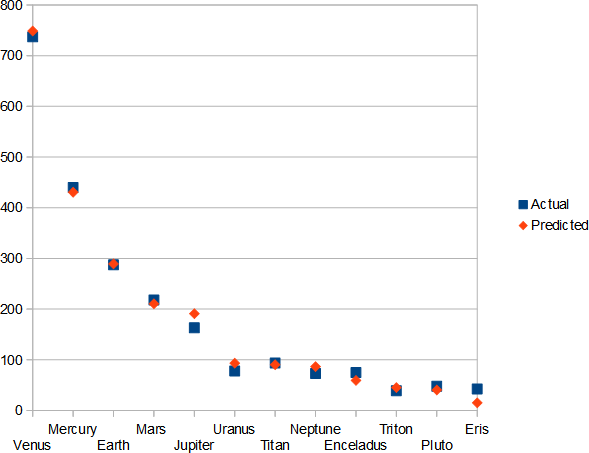
The RMS error is 15C – but as that is not atypical of the variation between surface temperatures from different sources it seems reasonable.
Discussion
Nikolov & Zeller identify that there appears to be a relationship between pressure and greenhouse temperature. They then use around a dozen different models, each with a couple of parameters and a limited subset of the available bodies which then then plot on a log log graph – when greenhouse temperature is known to be the log of the concentration. So in effect this is a log of a log – which is all but doing away with it altogether.
In contrast, I start with the blackbody temperature, then add on lapse rate calculated from the physical constant of heat capacity and the known height of 0.1bar level. The only “fudge factor” is to scale the greenhouse effect – and this is because I haven’t worked out how, or even if, I can calculate it.
However, please note, that saying greenhouse gas temperature goes up with pressure (as per Nikolov & Zeller), is also akin to saying that greenhouse temperature goes up with the height of the 0.1bar x lapse. (Which I suspect if I worked it out, would eliminate g and become a simple function of pressure). So, in that respect we are in agreement: greenhouse temperature is strongly related to pressure.
Conclusion
Contrary to Nikolov & Zeller, I find nothing to contradict the normal physics of the Greenhouse effect (at least when interpreted properly see: The Greenhouse Effect). Simply using the normal physics works well at predicting temperature across a large range of planetary bodies within the known inaccuracies. Moreover, the greenhouse effect needs to be included in those bodies with atmospheres low in GHGs in order to avoid substantial errors for those bodies.
Caveat
One caveat – on the further away bodies/less explored, it appears they may use a similar technique to calculate surface temperature. This, means on some bodies, that I may be effectively reversing the original method to calculate the surface pressure – so on these bodies we would expect a good match and it would not be an independent check on the methodology.


Re: ‘greenhouse temperature is strongly related to pressure.’
Any atmospheric temperature is ‘strongly related to pressure’ because temperature and pressure are directly proportional to each other. This relationship is called Gay-Lussac’s Law.
http://littleshop.physics.colostate.edu/activities/atmos2/TempPressureRelated.pdf
“Gay-Lussac’s Law.”
Yes indeed. Post modern physics wrongly treats gas kinetic energy as proportional to (mv²/2) with v being the rms of the Maxwell Boltzmann distribution of airborne molecules.
Newtons Kinetic energy\power is defined as the first derivative of that momentum never the integral; d(mv)/dt, never mv²/2. In all directions, at collision each of like molecules reverse their (mv in that direction), up to a 2mv change. This change is measured as temperature! Since that d(mv)dt is a function of 1/(mean free path), power/temperature increase with density. Gravitational ‘compression’, not acceleration, determines the static density of the atmosphere. OTOH nowhere is the atmosphere about Earth ever static. Compressed air is what powers air tools. For understanding anything, Oh woha are we! 🙂
I had an idea last night that the surface temperature could be calculated by starting out in the “blackness of space” at ~0k and then measuring the change in pressure as we moved down to the planetary surface.
I presume if we have P=f(T,h) if we turn it into T= f’ (h) we should get T = integral 0f (dT/dh) dh