I came across a couple of articles by Dr Roy Spencer on how greenhouse gases work and was surprised at both his answers and also the multitude of comments. There appears to be many diverse views on the theory, but do these matter in practice? To test this I propose to go through the various extreme cases of atmosphere to see whether others agree with the temperatures I derive. If not I would ask them to explain why they get a different answer.
Roy Spencer’s articles
What first prompted me to write this article is one by Roy Spencer : Why Atmospheric Pressure Cannot Explain the Elevated Surface Temperature of the Earth in which he appears to suggest that adiabatic warming doesn’t affect surface temperature. This is clearly wrong, so I started writing a letter to him to check whether whether I understood him correctly when I found another later article by him: What Causes the Greenhouse Effect? in which he seems to have changed his mind and agree that adiabatic lapse rate does affect surface temperature but now suggested adiabatic lapse is only caused by “greenhouse gases”. This also appears to be wrong, because the lapse rate is mainly a result of the adiabatic law:
P1-γ Tγ = constant
And so long as γ ≠ 1 , temperature will vary with pressure as it expands upwards. However keen observers may be thinking this only applies to a system where no work done. But if air rises it loses potential energy. So, each atom has less energy because it takes energy to raise the mass of the air against gravity. But fortunately, it all seems to work because the work done as the air expands exactly matches the loss in potential energy (however I digress).
So, to check whether there was a real difference in interpreation, I wanted to do is pose a number of hypothetical extreme case atmospheres, and ask whether those like Dr Spencer agree with the values I derive.
Hypothetical atmosphere
I wanted to minimise the complexity of my hypothetical planet to the minimum so that IR emitted from the surface and atmosphere could be treated entirely separately from incoming solar.
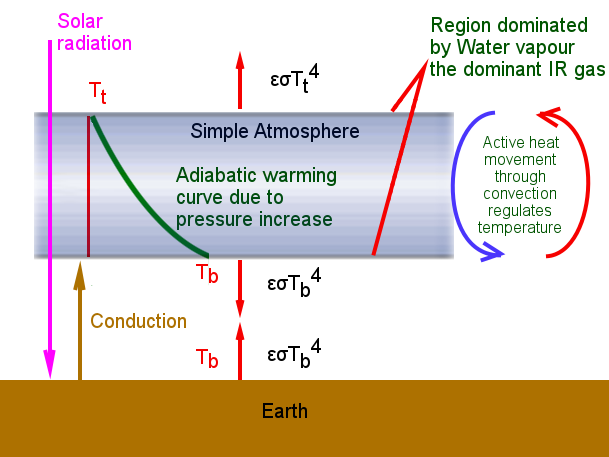
My hypothetical atmosphere based on the following diagram with the one major difference that the adiabatic lapse rate is assumed to be linear with height. Also please note the real atmosphere is in contact with the ground – whereas I drew a gap here so that I could show the various heat flows between the planet surface & atmosphere).
Simplified atmospheric model: transparent to visible, opaque to IR
Specification of the atmosphere (unless otherwise stated in example):
- Atmospheric Depth 10km
- Adiabatic lapse rate of 6.5C/km
- Infinitely fast/efficient convection circulation which maintains this adiabatic lapse rate irrespective of IR lost or gained from atmosphere.
- Blackbody equilibrium temperature of the planet without atmosphere: 250k
- Albedo: Planet surface is “black” so absorbs and emits at all wavelengths like a blackbody.
- Atmosphere depth neglibable: Planet is assumed to be so large that the extra 10km of atmosphere is too small to make any significant change in the surface area of the planet.
- Even insolation: Planet is assumed to be evenly illuminated by a number of of very hot suns so distant that they fill a negligible amount of the sky.
- Atmosphere is 100% transparent to radiation from outside. The suns assumed high enough temperature that the amount of IR is insignificant compared to higher wavelengths.
- Greenhouse gas: Atmosphere contains varying amounts of a gas. This gas absorbs and emits at all IR wavelengths so that when when dense enough at IR wavelengths it behaves like black body. But it is transparent to incoming radiation.
- No overlap IR & solar: We assume that at 250k all outgoing radiation is IR and does not overlap in frequency with incoming radiation.
- Infinite Test period (i.e. long enough so that surface of planet heats or cools to be in thermal equilibrium)
Test cases:
1. No Atmosphere
In this case, we are already told that the equilibrium temperature for the planet is 250k. This is the temperature at which incoming solar radiation balances with emitted IR radiation.
2. Atmosphere 100% transparent
We now introduce an atmosphere which does not absorb or emit IR. It still has a 6.5C/km lapse rate. Now the atmosphere is transparent to both incoming solar radiation and outgoing IR. It neither absorbs incoming radiation nor outgoing radiation.
In this case, as the atmosphere does not interact with outgoing IR radiation and because incoming solar radiation and outgoing radiation must balance, the surface will be at the equilibrium temperature of a blackbody at 250k. The temperature of the top of the atmosphere can now be calculated using the lapse rate as being 250 – 65 = 185k
3. Atmosphere 100% opaque to IR.
In this case the atmosphere is so opaque to radiation from the surface that the only IR radiation that escapes is from the very top of the atmosphere. Now the energy must balance at the top of the atmosphere and so now the top of the atmosphere must be in equilibrium so that outgoing IR matches incoming solar radiation.
At this surface, the temperature must be the same as the blackbody temperature of 250k.
With a 6.5C/km lapse rate from the top to the bottom of the atmosphere, the surface temperature will be 250k + 65k = 315k
4. Atmosphere which is transparent except for a thin band at height z which is 100% opaque.
In this case the atmosphere only emits and absorbs at the opaque layer at height y. Therefore this layer will be at the blackbody temperature of 250K. The distance to the surface is y, so the adiabatic lapse rate is given by
Temperature = 250 + 6.5 y
Here we can see that we obtain case (2) if y is zero and case (3) if y is 10km
5. Atmosphere where IR from space is emitted or “seen” equally from all layers of the atmosphere.
We assume the greenhouse gas concentration is such that if the atmosphere were at a uniform temperature, that IR would be emitted equally from all layers of the atmosphere to space.
[Also for simplicity I am assuming the average temperature “seen” is the average of the temperature. In fact it is the average of T4]
But the atmospheric temperature varies from surface upward with a lapse rate of 6.5C/km. So, in this case, the average temperature as “seen” from space will be the black body temperature of 250k. And the average lapse rate to the various layers of the atmosphere is the average from the top and bottom of the atmosphere of: (0 + 10 x 65)/2 or 32.5K. So the temperature at the surface will be 282.5K
‘No atmosphere – In this case, we are already told that the equilibrium temperature for the planet is 250k.’
But Diviner data for the ‘no atmosphere’ Moon, which obviously is the same distance from the Sun as Earth (on average), pointed to a figure of 197K.
https://tallbloke.wordpress.com/2012/05/01/ned-nikolov-implications-of-diviner-results-for-the-s-b-standard-equation/
Earth is mostly covered with water.
The ocean have boiled in the distant past [and I believe they have never completely frozen since] so one start with ocean being say 20 C [average temperature] and with surface at 20 C.
Or if you like with last 50 million years the average ocean temperature has be at least 10 C,
so start with 10 C. Land area which only 30% can be ignored in order to simplify it.
You try to simplify, bur over-simplify to the point of absurdity! None of your cases are physically realizable! This Earth’s atmosphere is not simple, but perhaps the most complex fluid dynamics situation ever encountered! It is not “explain in one paragraph, and give three examples”. For Atmospheric Physics 101, start with 200 Navier-Stokes partial differential equations, with only 8 orthogonal variables. This is not to discourage learning, as long as learning is the “goal”.
Do not expect “knowledge”! Way to many out there promoting their religion! Beware any that claim knowledge! Run, do not walk, away from any University Professor!
The 250k is an arbitrary number – chosen to be roughly the same as the earth. But it’s clearly not the earth as it has at least four suns and there’s no moon.
What I’m trying to understand is whether the disagreement is on the fundamental laws of physics, or whether it is just how to apply them in the specific instance of the earth.
Or perhaps it is all semantics: in other words, two people might describe a problem in different ways and come to the same physical numbers.
I’ve given a range of test cases which should be easy to work out and this will help me understand whether it’s a difference in the meaning of words – without a real physical difference, or whether the apparent arguments over semantics do represent different actual physical predictions.
1. No Atmosphere
In this case, we are already told that the equilibrium temperature for the planet is 250k. This is the temperature at which incoming solar radiation balances with emitted IR radiation.
We are told this by folk with no competence in such a subject,. Moon conditions, hot sunside,
cold niteside, very cold poles. Radiatively some average temperature has absolutely no meaning, Missing here is the spectral and angular emissivity of the surface With high SW emissivity and low LW emissivity, quite high temperature! No one has measured such.
[“You are correct that the various temperatures and surfaces adjust to exactly emit to space all insolation absorbed. This is called radiative equilibrium.”
Jan:Please move this up to be part of my response to #1 Sorry – hopefully in the right place!, Mike]
2. Atmosphere 100% transparent
We now introduce an atmosphere which does not absorb or emit IR. It still has a 6.5C/km lapse rate. Now the atmosphere is transparent to both incoming solar radiation and outgoing IR. It neither absorbs incoming radiation nor outgoing radiation. You are correct that the various temperatures and surfaces adjust to exactly emit to space all insolation absorbed. This is called radiative equilibrium.
In this case, as the atmosphere does not interact with outgoing IR radiation and because incoming solar radiation and outgoing radiation must balance, the surface will be at the equilibrium temperature of a blackbody at 250k. The temperature of the top of the atmosphere can now be calculated using the lapse rate as being 250 – 65 = 185k
Even N2, 10-60 km thick would have some emissivity at each frequency! All the ifs of #1 remain! The actual spectral opacity of the whole atmosphere also has never been measured. On this planet the opacity of airborne water condensate and the huge “atmospheric latent heat” generated sunside and released to space niteside dominate all other radiative effects. This Earth needs no surface!
Scottish Sceptic,
Simple examples like these are good for testing understanding and illustrating principles. I agree with you on 1, 3, and 4, but you have made an error in 2. Heat flows from high T to low T, so the lapse rate produces a vertical flow of heat. The energy can not escape from the upper atmosphere, so it accumulates and causes the temperature to rise until the lapse rate is zero and the heat transfer stops. So the T at TOA is 250 K, just like at the surface.
I am not sure about 5, since I don’t see a simple way to get the lapse rate.
“You are correct that the various temperatures and surfaces adjust to exactly emit to space all insolation absorbed. This is called radiative equilibrium.”
Please move this up to be part of my response to #1 Sorry
“Heat flows from high T to low T, so the lapse rate produces a vertical flow of heat.”
Not in this atmosphere! Spontanious energy transfer does not occur in a direction of higher potential 2LTD. Gravitational potential negates both the pressure and temperature gradients in this atmosphere.
Will thanks for the comments
1. this is a test case whereby however you think planetary heating works, you asked to adjust your values so that this hypothetical planet starts at a uniform temperature of 250K.
Whatever your model of planetary heating, I’m asking you to start by adjusting that to give a uniform temperature of 250k so that we all start with a temperature we agree with.
2. Of course it’s not a real atmosphere. Instead it is a hypothetical atmosphere intended to test whether your concept of warming is the same as mine when there is no IR interaction.
Thanks. but surely the lapse rate is really a measurement of the average potential energy lost as atoms move upward? So, each atom gains energy as it falls and loses energy as it rises. So, if we imagine each atom bouncing up and down in a layer – there is a minute difference in temperature between collisions as it hits the layer below and those as it hits the layer above. Over many kms this small difference amounts to around 9.8C/km
This isn’t the 6.5C, but I assume it would be on a lower gravity planet.
Scottish Sceptic,
“but surely the lapse rate is really a measurement of the average potential energy lost as atoms move upward?”
No, it’s not. The adiabatic lapse rate is a measurement of when the temperature gradient is sufficient to drive strong convection. The second Law of Thermodynamics says that heat flows from hot to cold. So the T gradient gives you the direction of heat flow and the heat flow will reduce the gradient, unless something acts to maintain the gradient.
Convection increases very rapidly when the T gradient exceeds the adiabatic lapse rate and that strong convection reduces the T gradient. As a result, the gradient can never be much larger than the adiabatic lapse rate.
Scottish Sceptic,
In the spirit of your test cases, here is another test case. We construct the following device on your hypothetical planet, case 1, no atmosphere. The device has a very large, thick, horizontal copper plate; the idea is that it is highly conductive so as to be at a uniform temperature of 250 K. Attached to this plate are two equal height vertical tubes, the walls of which are made of some effectively non-conductive material. One tube is filled with He, mole weight 4; the other is filled with Xe, mole wt 131.
I say that the temperature of the gas near the tops of the tubes is the same in both tubes. What say you?
I read your comments last night. So far I only needed to know the lapse rate existed and wasn’t too concerned why. But as a result of your comment I decided to check I understood the lapse rate properly.
After checking I was right I wrote the following article: http://scottishsceptic.co.uk/2015/07/03/what-is-the-adiabatic-lapse-rate-of-air/ in which I try to explain why the lapse rate is a result of potential energy loss.
First, implicit in the question is that the lapse rate is no longer fixed but is a result of the gases. Neither gas has water, so the lapse rate is just g /Cp (g gravity, Cp heat capacity per kg).
That suggests a different thermal gradient, but at some point it seems we get a “top” to the bulk of the atmosphere and then an isothermal region. A hand waving argument suggests that the effective temperature as seen from space of the planet must be the same whatever the gas, but as at least part has a different lapse rate, I’m not able to predict the exact thermal gradients that would exist so I cannot say where the “top” would be, Also, as the temperature of the top dictates the ground temperature and not visa versa, it’s a little difficult to know how to answer your question meaningfully.
Scottish Sceptic,
It seems I failed to make myself clear. He and Xe do not absorb IR (or any other part of the spectrum of interest). So the situation in the tubes is that of your case 2.
You wrote: “the temperature of the top dictates the ground temperature and not visa versa”. But that is ot what you said in analyzing case 2.
Also, my question only requires a qualitative answer. Which applies at the tops of the columns?
(a) Xe is warmer than He
(b) Xe is the same temperature as He
(c) Xe is colder than He
I should add that since He and Xe are both noble gases, they have the same molar heat capacity. So the heat capacity per kg is greater for He than for Xe.
OK, that makes more sense.
And if it is transparent then quite right the statement “the temperature of the top dictates the ground … ” is wrong.
If they had the same heat capacity per **KG** then they would have the same lapse rate, but checking online I find that Cp for Xe is 0.16 kj/(kg k) and for He is 5.19 (but these are constant pressure – not quite right – but I use anyway). So the lapse rate of Xe would be ~=9.8/0.16 or 56k/km and that for He is 9.8/5.19 ~=1.9k/km
Helium has a molar mass of 4, xenon 131, so ~33x so most of the difference in lapse rates is accounted for by the difference in molar mass.
Scottish Sceptic,
So you are plunking for (c) Xe is colder than He at the tops of the columns?
So now, what will happen if I tie the tops of the columns together with an excellent thermal conductor that is in contact with the gases at each end?
You might be starting to realize that this is going somewhere uncomfortable.
I only just noticed your 8:45 response and checked out the link. I think I will explain the flaw in that argument in the comments on that page.
Mike, if the tops are tied together, then the temperature at the tops would be the same and one would tend to cool and the other warm. Then all kinds of things happen including change in pressure which may mean one gas is no longer in contact and potential convection currents.
Scottish Sceptic,
You can do better than that. You are right that the connection will make the top of the Xe column warmer and the He column cooler. But when you displace a system from equilibrium, it will try to re-establish that equilibrium. So heat will flow up the He column, down the Xe column, and through the metal plate connecting them. Forever. That is perpetual motion.
You might object that it is only heat that is flowing, there is no actual motion. So put a thermal electric generator in the connection between the tops of the columns. Now you have an infinite source of electricity. Clear violation of the Second Law.
Your claim as to what controls vertical T gradients is thus conclusively proven wrong.
OK, I see what you are getting at, but simple conservation of energy tells us the temperature must drop as we rise.
Initially you are right that heat would flow up one and into the other and it would be interesting to know how it stabilises.
My guess is that the one with a lower top temperature would see a rise in temperature and that would cause a rise in gas pressure and a change in the specific heat capacity so that it then becomes stable with no net change in temperature.
“simple conservation of energy tells us the temperature must drop as we rise.”
Not so. Does it get cold inside an airplane when it climbs?
When a gas expands against a resisting pressure, it will cool. That is true whether or not it is rising. The reduction in internal energy (cooling) is due to doing work, but the work is being done against the resisting pressure. The fact that you can, under appropriate circumstances, use that work to lift something is not really relevant.
If the origin of the adiabatic lapse rate is as you say, then how could we have a smaller lapse rate? But that is common; the dry adiabatic lapse rate is 9.8 K/km, but the average lapse rate is only about 6.5 K/km. Yes, the wet adiabatic lapse rate is smaller than the dry adiabatic lapse rate, but clouds occupy only a small portion of the troposphere and the wet lapse rate applies only when water is condensing.
We can even have a negative lapse rate (T increases with height) under temperature inversions or everywhere in the stratosphere.
When molecules are in a gravitational field, they loose energy as they rise up against that field and increase it as they drop. If that didn’t happen we wouldn’t have an atmosphere as any molecule hit upwards would just continue upwards and so leave the atmosphere.
Saying that heat reduces is really just like saying pressure reduces. It’s just inherent in a gas in a gravitational field. But that is not the same as saying that external sources of energy cannot change that temperature gradient.
As for the smaller lapse rate, that is because the air is moist and energy is being gained from the condensation of water vapour.
‘Not so. Does it get cold inside an airplane when it climbs?’
Sorry but this is an obvious dud. Cabins are pressurised and heated based on the Standard Atmosphere.
http://www.digitaldutch.com/atmoscalc/help.htm