Lies, damned lies, and statistical significance of climate trends

Today I read another article talking about “statistically significant warming” (link) and I wondered how anyone could know what is statistically significant without knowing the nature of the underlying natural variation.
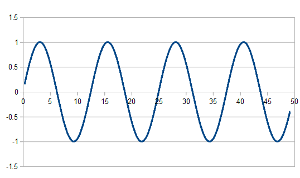So, let’s introduce a very simple model of some underlying natural variation. The scenario is that we are measuring water level and that natural variation is giving +/-1m of variation occurring every 12-13 hours.
As can be seen, there isn’t much else going on except this natural variation.
Now let’s suppose that we want to detect whether there has been some “significant change” to this variation.
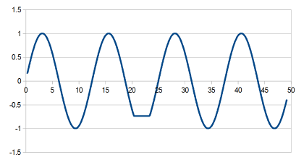For this I will use the example to the right. It is very obvious to us as observers that something unusual has happened. The tide has failed to go out!
But unfortunately, if we were checking this with almost all statistical tests, it would be almost impossible to detect it. Why? The reason is simple. The scale of the natural variation is around +/-1 m. But the “blip” we are looking at is well within that scale. Nor is the trend of zero unusual. So, if our model of “natural variation” only includes the scale of variation and trend, then nothing at all is unusual with the example.
But you exclaim – this isn’t random – so it’s not fair!
OK, let me now introduce a random example. Let me use an example similar to “the significance of a flood event”, but this time I will be asking how statistically significant it is if the water reaches a particular level and this time it is entirely random.
In this example, I fill up a jug with a random amount of water and pour it into a bath with a sealed plug holes.  How statistically significant is it if the bathroom has a flood?
The answer of course, is that sooner or later the bath will overflow. So, at the 95% confidence limit …. it will flood, so will it at the 25% confidence limit or even 100% confidence limit.
So, if it overflows what does this tell us about whether or not there was some non-random input such as adding a few extra gallons? In this case, it is now certain the bath will overflow, so the fact it overflows tells us no added information.
“But that’s cheating” you say – “because the bath only fills with water”.
OK, so now let’s start filling the bath and taking it out. But this time, I will start by filling the bath with a jug with a random amount of water, then I will take out a random amount of water. This is now what is officially called a “random walk” (almost). And statistically the bath will gradually fill up with water approximately proportional to the square root of the number of cycles. (I start with nothing so it can’t get less).
Now, it is entirely random, but statistically, sooner or later it will overflow. Because sooner or later there will be a run of jugs whereby the total excess put into the bath exceeds the amount taken out of the bath by the volume of the bath and it will overflow. So, yet again how statistically significant is it if the bath overflows? Again it is certain it will, it will just take longer than the previous example, but sooner or later it will happen.

Statistical Significance is meaningless if you don’t understand the form of the variation

This is why it is so important to understand the nature of the “normal” behaviour of a system before applying Noddy statistical tests. The point I’m making is that if you don’t understand the “natural variation” of a system and how that variation affects the system, then how can you exclude any of the models of variation I have given above where statistical significance is almost meaningless without reference to the model.
So, e.g. if we know the tide, we can see that the first case is a statistically significant variation from the expected behaviour. But if we don’t have a model for the way tides ebb and flow, then we do not know what is “normal” so cannot know what is “abnormal”. Likewise if the underlying natural variation continually increases, or if it contains long term trends.
And this is well known. For example if we look at another WUWT article: No statistically significant warming since 1995: a quick mathematical proof
and look at the page they refer on the statistical test: Stat Trek and look at the stated requirements for this test, we see it clearly spelt out that it is not suitable for systems where one year’s results tend to be similar to the preceding year:

The approach described in this lesson is valid whenever the standard requirements for simple linear regression are met.

• The dependent variable Y has a linear relationship to the independent variable X.
• For each value of X, the probability distribution of Y has the same standard deviation σ.
• For any given value of X,
  • The Y values are independent.
  • The Y values are roughly normally distributed (i.e., symmetric and unimodal). A little skewness is ok if the sample size is large.

So, it must be just as likely after a warm year that we get a cold year. That means we cannot get periods of natural variation with colder climate like the little ice-age, nor periods of warmer climate like the Medieval warm period.
So, basically, what they are saying is that it is/isn’t statistically significant – so long as the climate doesn’t behave like the climate.
Which is akin to saying: if you use noddy statistics which should never be used, you may prove whatever you might want to prove.

Lies, damned lies, and statistical significance of climate variations